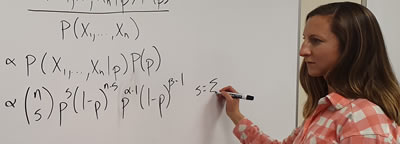
Bayesian Short Course

2024 Short Course on Bayesian Models for Ecologists

The fundamental challenge of science is to develop lines of inference connecting novel questions to new insights properly tempered by uncertainty.  Reliable inference depends on using mathematical and statistical models to determine the value of data as evidence. It follows that skills for making inference based on models and data are a requirement for doing successful science.

Colorado State University will host a 10 day short course “Bayesian Models for Ecological Data” from June 3 – June 13, 2024 covering basic principles of using Bayesian models to gain insight from data. An award from the Population and Community Ecology Program of the the National Science Foundation to Colorado State University will cover costs of lodging and meals during the course. There is no tuition.  We will also cover up to $500 in costs of transportation to the course for graduate students, but not for post-docs or more established ecologists. The course is aimed at doctoral students, postdocs, agency researchers, and university faculty from US institutions.

The goals of the course are to:

1. Provide a principles-based understanding of Bayesian methods needed to train students, evaluate papers and proposals, and solve research problems.
2. Communicate the statistical concepts and vocabulary needed to foster collaboration between ecologists and statisticians.
3. Provide the conceptual foundations and quantitative confidence needed for self-teaching modern analytic methods.

Click here to apply

Short Course Overview

The course will include lectures and laboratory exercises. Labs will emphasize problem solving requiring programming in R and JAGS. The course will enable participants to:

1. Explain key principles of Bayesian statistics, including the concepts of joint, conditional, and marginal probabilities; posterior and prior distributions; likelihood; conjugacy; and the relationship between Bayesian and maximum likelihood approaches to inference.
2. Use basic statistical distributions (e.g., binomial, Poisson, normal, log normal, multinomial, beta, Dirichlet, gamma, multivariate normal) to write joint and conditional posterior distributions for hierarchical Bayesian models that couple models of socio-ecological processes, models of data, and random effects.
3. Explain how Markov chain Monte Carlo (MCMC) methods can be used to fit Bayesian models to data.
4. Write algorithms and computer code in R implementing MCMC methods to fit simple models.
5. Use JAGS software to implement MCMC methods to find posterior distributions of parameters, latent states, and derived quantities.
6. Evaluate model convergence and assess goodness of fit of models to data.
7. Develop and implement hierarchical models that explicitly partition uncertainties.
8. Understand the basis for statistical inference from single and multiple Bayesian models.
9. Use Bayesian methods to synthesize results from multiple scientific studies.
10. Understand Bayesian methods for modeling spatially structured data.